ResNeXt

Aggregated Residual Transformations for Deep Neural Networks

Introduction

作者介绍了谷歌的Inception module的工作，指出该module是通过\(1*1\)的卷积将输入拆分出低维的嵌入，然后再通过特定的卷积核之后将得到的向量特征图拼接在一起。但是该模型有一个缺点，需要人为手动去设计每一层，较为繁琐。所以本篇文章提出的ResNeXt是将resnet和inception的特点结合起来。

Method

Template

新的backbone仍然遵守以下两点规则：

• 如果生成了相同大小的特征图，那么模块共享相同的超参
• 每一次特征图经历了两倍下采样，通道就要增加一倍（保证了计算的复杂度）

Revisiting Simple Neurons

标准神经元公式可以被描述为：\(\sum_{i=1}^D w_ix_i\)

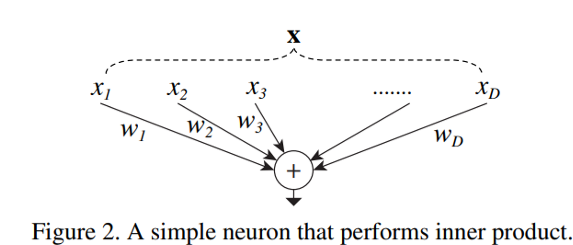
神经元的操作可以被概括为：

• 分割，x向量被分割成许多低维嵌入
• 转换，低维的嵌入与权重相乘
• 汇总，最终将得到的结果求和

Aggregated Transformations

将上小节公式拓展为一般形式：

$$
F(x)=∑_{i=1}^CT_i (x)
$$

其中T_i(x)可以为任意形式，C是转换公式的个数，这里的C可以为上小节的D，但它并不需要是这样，在本篇论文中为了设计方便所有的T都具有相同的拓扑结构如下右图所示：

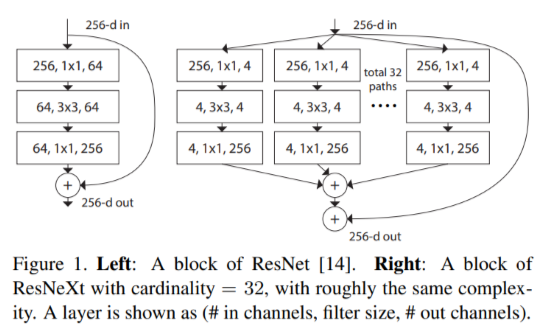
在此拓扑结构中首先需要将特征图经过\(1*1\)的卷积层调整成低维通道数。上图的公式可以表示为：

$$
y=x+∑_{i=1}^CT_i (x)
$$

Relation to Inception-ResNet

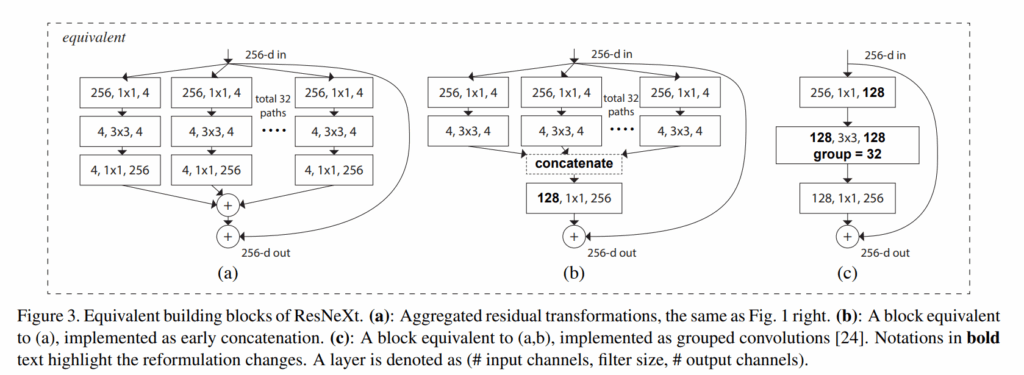
上式三图是等效的，虽然第二幅图与Inception-resnet结构很像，但还是有很大的区别，每一个block的路径所使用的结构是相等的。

Relation to Grouped Convolutions

上述第三幅图和第一幅图等效，说明在实现的时候可以选择组卷积的方式去实现

可以注意到这样的结构只有在深度大于3的时候才能具有拓扑结构，如果深度只有2的话就仍然是一种具有高维通道数的密集模型。如下图所示：

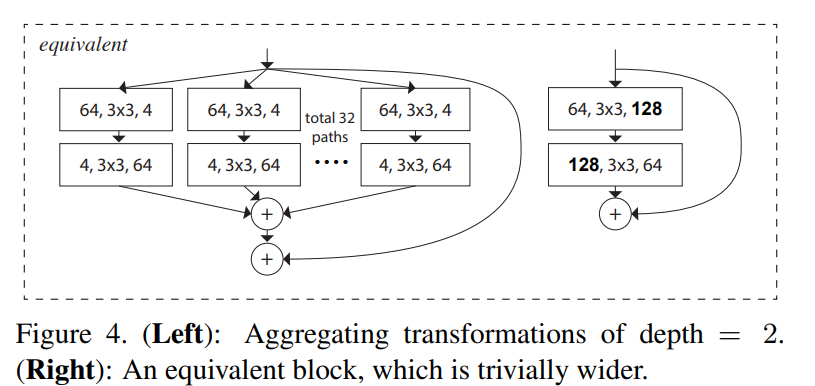
Model Capacity

为了验证不同的C基数对效果的影响，首先需要保持计算复杂度相差不大，普通resnet bottle block

$$
256⋅64+3⋅3⋅64⋅64+64⋅256≈70k
$$

本文的block：

$$
C⋅(256⋅d+3 ⋅3⋅d⋅d+d⋅256)
$$

为了保持计算量相对稳定,C和d的关系如下所示：