DeformConv

Deformable Convolutional Networks

Introduction

在视觉识别中如何让模型去适应大小，视角，姿态不同，或者部分形变的目标。目前主流的做法有两种：

• 通过数据集增强
• 使用一些具有变化不变性的特征或算法

但是上述两种方式又有各自的缺点：

• 通过数据集增强的这些变化都是已知的，无法应对未知的变化
• 涉及算法有时会过于困难

然而CNN的这两个弱点全部都被占了。因此在本篇文章中，设计了两种模块来弥补这一缺点：

• deformable convolution，给每个卷积通道的预测后加了二维偏移
• deformable RoI pooling，在每个bin后加了二维偏移

Deformable Convolutional Networks

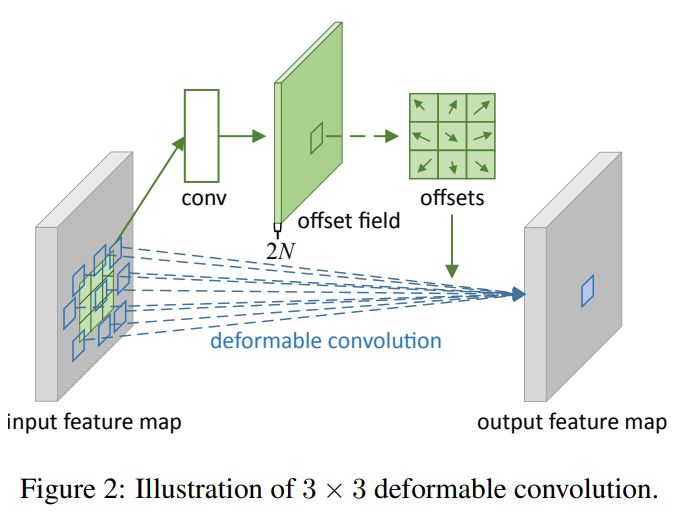
Deformable Convolution

普通的卷积操作通常分为两步：

• 在feature map上确定采样区域R
• 利用卷积核上的权重进行求和

公式表示为：

$$
y(p_0)=∑_{p_n\in R}w(p_n )⋅x(p_0+p_n)
$$

其中\(p_0\)为最终输出的位置（卷积核中心对应的输入特征图的位置），\(p_n\)对应卷积核覆盖的输入区域。Deformable Convolution额外加入了偏移的指标，表达式为：

$$
y(p_0 )=∑_{p_n\in R}w(p_n )⋅x(p_0+p_n+Δp_n ),\{Δp_n│n=1,…,N\}, N=|R|
$$

其中,\(R\)为卷积核的大小，由于\(\Delta p_n\)可以是小数，所以上式需要通过双线性插值的方法来完成：

$$
x(p)=∑_qG(q,p)⋅x(q),p=p_0+p_n+Δp_n
$$

\(q\)为输入的特征图中所有整数的坐标值，\(G(,)\)双线性插值的内核，由于其是两维的，所以可以分别将它们分成一维：

$$
G(q,p)=g(q_x,p_x )⋅g(q_y,p_y ),g(a,b)=max⁡(0,1−|a−b|)
$$

关于\(\Delta p_n\)的反向传播算法：

$$
\frac{∂y(p_0)}{∂Δp_n}∑_{p_n\in R}w(p_n)⋅\frac{∂x(p_0+p_n+Δp_n)}{∂Δp_n}=∑_{p_n\in R}[w(p_n )⋅∑_q\frac{∂G(q,p_0+p_n+Δp_n)}{∂Δp_n}x(q)]
$$

Deformable RoI Pooling

RoI pooling:普通的RoI pooling若\(x\)为输入的特征图，RoI左上角为\(p_0\)，RoI最终输出的尺寸为\(k\times k\)，\(n_{ij}\)为每个bin内像素点的个数，则第(i,j)个bin的表达式可以写为：

$$
y(i,j)=\frac{∑_{p∈bin(i,j)}x(p_0+p)}{n_ij}，⌊i w/k⌋≤p_x≤⌊(i+1)w/k⌋;⌊jhk⌋≤p_y≤⌊(j+1)hk⌋
$$

Deformable RoI Pooling：

$$
y(i,j)=\frac{∑_{p∈bin(i,j)}x(p_0+p+Δp_{ij})}{n_ij}
$$

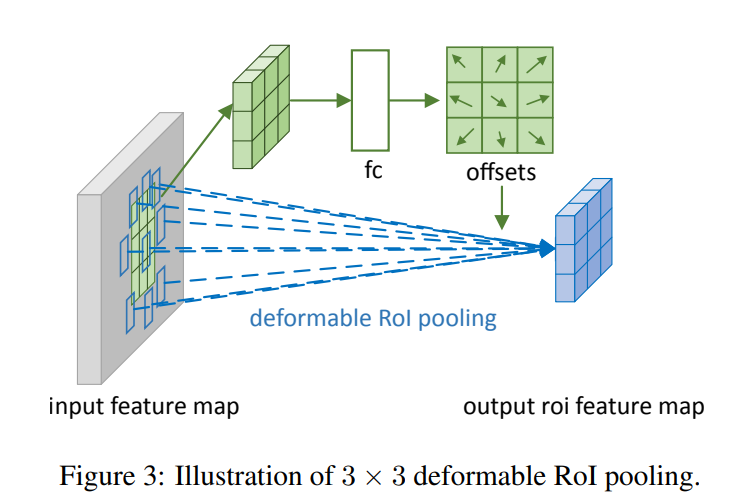
如下图可以知道大致的工作流程：

首先通过RoI pooling产生特征图，之后再利用全连接层预测标准化的偏差\(\Delta\hat{p}_{ij}\)，以及公式\(\Delta p_{ij}=\gamma \Delta\hat p_{ij}∘(w,h)\)，\(\gamma=0.1\)将其转换为实际偏差。

反向传播的流程为：

$$
\frac{∂y(i,j)}{∂Δp_{ij}}=1/n_{ij}∑_{p\in bin(i,j)}\frac{∂x(p_0+p+Δp_{ij})}{∂Δp_{ij}}=1/n_{ij} ∑_{p\in bin(i,j)} [∑_q\frac{∂G(q,p_0+p+Δp_{ij})}{∂Δp_{ij}}x(q)]
$$

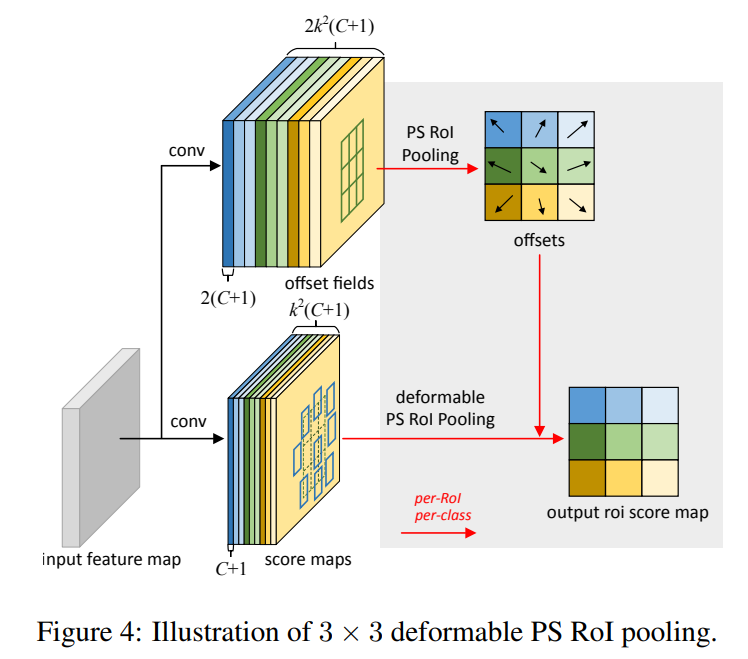
Position-Sensitive (PS) RoI Pooling:

不同于RoI pooling，它是全卷积的。输入的特征图经过全卷积层，每一个种类都会被分\(k^2\)个通道，来代表之前的\(k^2\)个小块（这里涉及到了一个R-FCN的一个知识点，每个通道上只代表一个小方块的特征图），每个通道的feature map可以表示为\(x_i\)，最终每个bin内的值就是其对应通道值和的均值，与Deformable RoI Pooling预测的不同指出在于它给每个通道都预测了偏差，但是偏差的计算方法都是相同的。并且公式上的不同之处在于将x换成了\(x_{ij}\)。

​

​