GWD

xyh
CV
2021-07-28
92热度
0评论

Rethinking Rotated Object Detection with Gaussian Wasserstein Distance Loss

Introduction

旋转目标检测作者总结出来的难点有以下几点：

loss和指标的不一致（loss可能没法反应出最终的指标效果）
边界的不连续性
边界框如果是正方形的话会影响最终的检测效果

这篇文章的主要贡献：

总结了关于旋转目标检测的三个难点
将GWD （Gaussian Wasserstein Distance）即推土机距离引入模型中
利用GWD去解决之前提到的问题
模型结果在众多数据集中取得了不错的表现

Rotated Object Regression Detector Revisit

首先基于角度回归分析旋转目标检测器的一些缺陷：

Bounding Box Definition

旋转目标利用角度回归的检测其中对于角度的处理通常有两种方法：

opencv定义法$D_{oc}$
基于长边的定义方法$D_{le}$

$$
D_{le}(h_{le},w_{le},θ_{le})= \begin{cases} D_{oc}(h_{oc},w_{oc},θ_{oc}), & h_{oc}\ge w_{oc} \\ D_{oc} (w_{oc},h_{oc},θ_{oc}+90°), &\text{otherwise} \end{cases}
$$

$$
D_{oc}(h_{oc},w_{oc},θ_{oc})= \begin{cases} D_{le}(h_{le},w_{le},θ_{le}), & \theta_{le}\in [-90°, 0) \\ D_{le} (w_{le},h_{le},θ_{le}-90°), &\text{otherwise} \end{cases}
$$

作者在之前的论文中提出过使用角度回归的三个问题，分别为PoA（角度的周期性），EoE（边界的变换），square-like problem（长宽比接近带来的问题），如果使用的是长边定义法可以将边界变换的问题解决，但是治标不治本。

Inconsistency between Metric and Loss

通过列举不同IoUloss来说明旋转目标检测性能指标和loss会出现不一致的情况

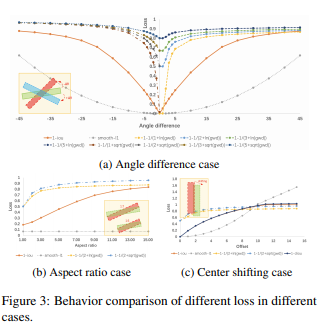
case1：比较IoU loss和smooth l1 loss 不仅可以看出loss和指标的不一致，还可以发现旋转目标的IoU loss确实不可导。

case2：比较IoU loss和smooth l1 loss 随着长宽比的增长smooth l1 loss却一直是常数常数但是IOU的增长趋势变化相对较大

case3：两者的loss单调性是一样的，但是高度不是完全一致。

Boundary Discontinuity and Square-Like Problem

开始介绍边界不连续和长宽比过于接近的问题：

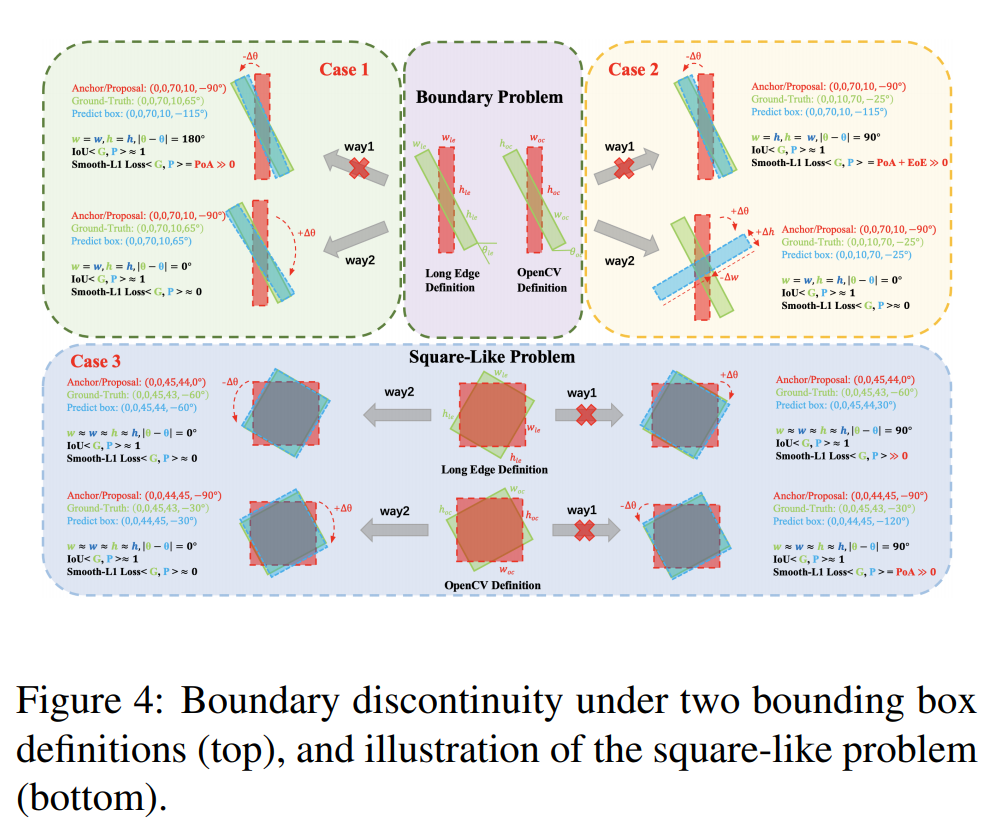
拿上图case2 opencv定义方法举例说明红色anchor/proposal（0，0，70，10，-90），绿色gt为（0，0，10，70，-25），那么模型可能很容易按照way1的方法去预测这样会出现PoA和EoE的问题，最终导致的结果就是实际loss过大，这种情况下模型的预测只能朝着way2的方向发展，这样会使得模型进行更为复杂的回归。

但是作者又指出如果预定义的anchor/proposal不在角度边界处，那么way1不会出现太大的loss；除此之外，还需要分析一下square-like problem，在case3中，使用长边定义的方法红色anchor/proposal(0，0，45，44，0)，绿色的gt为（0，0，45，43，-60）如果预测的蓝色box为（0，0，45，44，30）虽然效果上应该不会有太多问题，但是实际上仍然会有较大的loss值，所以在回归的时候还是需要绕一大圈让模型进行复杂的回归，这一问题不是由PoA或者EoE所引起的，而是由loss和指标的不连续性所引起的

The proposed Method

接下来要介绍的方法需要满足以下三个条件：

IoU和指标的高度一致性
可以直接求导学习
在边界处平滑

Wasserstein Distance for Rotating Box

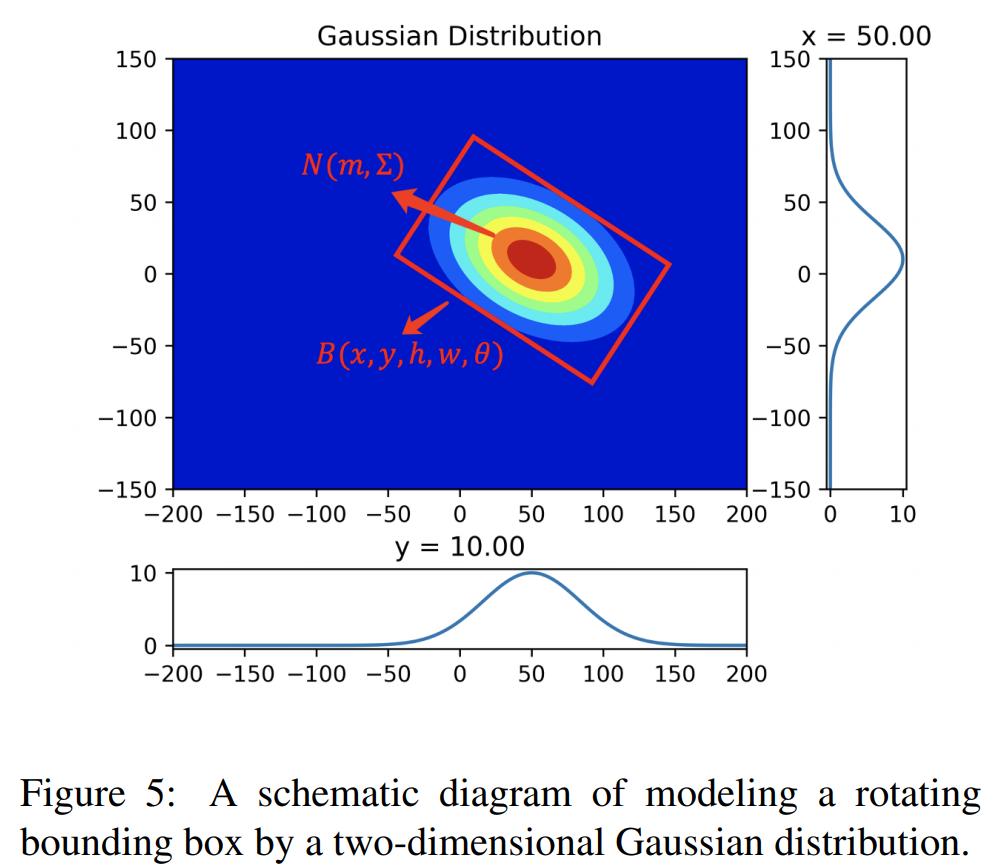
rotate box的高斯分布均值和方差如下所示：

$$
m=(x,y)\\ Σ^{1/2}=RSR^T= \begin{pmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{pmatrix} \begin{pmatrix} w/2 & 0 \\ 0 & h/2 \end{pmatrix} \begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix} \\= \begin{pmatrix} \frac{w}{2}cos^2⁡θ+\frac{h}{2}sin^2⁡θ & \frac{w-h}{2}cos\theta sin\theta \\ \frac{w-h}{2}cos\theta sin\theta & \frac{w}{2}sin^2⁡θ+\frac{h}{2}cos^2⁡θ \end{pmatrix}
$$

其中R是旋转矩阵S表示特征值的对角矩阵

GWD的一般表达式为

$$
W(μ;v)≔infE(‖X−Y‖)^{1/2}
$$

两个分布均为正态分布，可以表示为：

$$
d^2=‖m_1−m_2 ‖_2^2+Tr(Σ_1+Σ_2−2(Σ_1^{1/2} Σ_2 Σ_1^{1/2})^{1/2})
$$

最终经过推导表达式可以写为

$$
d^2=l_2−norm([x_1,y_1,w_1/2,h_1/2]^T,[x_2,y_2,w_2/2,h_2/2]^T )
$$

Gaussian Wasserstein Distance Regression Loss

如果直接将该距离应用到损失函数中效果其实并不好（后续实验可以证明）所以利用IoU loss的形式加入到损失函数中：

$$
L_{gwd}=1−1/(τ+f(d^2 ) ), τ≥1
$$

其中f为非线性函数的功能为ln或者sqrt

到目前为止该损失函数满足上述三个条件中的前两个，为了满足第三个条件还需要发掘函数本身的三个定义：

$$
Property 1:Σ^{1/2} (w,hθ)=Σ^{1/2} (hw,θ−π/2)\\ Property 2:Σ^{1/2} (w,hθ)=Σ^{1/2} (w,h,θ−π)\\ Property 3:Σ^{1/2} (w,hθ)≈Σ^{1/2} (w,h,θ−π/2),if\quad w≈h
$$

由性质1可以发现不论是opencv定义法还是长边定义法在GWD loss中是等价的，所以不需要特别纠结角度的对应关系，所以GWD不需要特别绑定某一类的角度定义方法，并且根据这些性质可以发现它们可以有效的解决上述问题。

GWD的好处主要有：