KLD

xyh
CV
2021-08-04
79热度
0评论

Learning High-Precision Bounding Box for Rotated Object Detection via Kullback-Leibler Divergence

Introduction

本篇文章的四大亮点：

不同于传统的旋转检测器，本文提出新的旋转检测损失函数，并且该损失函数可以退化成水平方向检测的损失函数；
使用了KL散度来度量两个高斯分布间的距离；
通过梯度分析KL散度发现它的自适应调整机制非常好用；
通过实验证明了提出的loss的卓越性。

Background

Inductive Thinking of Loss Design: from Special Horizon to General Rotation Detection

之前旋转检测器的loss损失函数都是通过归纳的方法（从特殊到一般）：

$$
t^p_x=\frac{x_p-x_a}{w_a}\quad t^p_y=\frac{y_p-y_a}{h_a}\quad t_w^p=ln(\frac{w_p}{w_a})\quad t_h^p=ln(\frac{h_p}{h_a})\\ t^t_x=\frac{x_t-x_a}{w_a}\quad t^t_y=\frac{y_t-y_a}{h_a}\quad t_w^t=ln(\frac{w_t}{w_a})\quad t_h^t=ln(\frac{h_t}{h_a})\\
$$

可以归纳出最后损失函数通常为:

$$
L_{reg}=l_n-norm(\Delta t_x,\Delta t_y,\Delta t_w,\Delta t_h,\Delta t_{\theta})
$$

可以看出损失函数是在独立的调节每个参数的，使得损失函数对于每个参数都很敏感。

Deductive Thinking of Loss Design: from General Rotation to Special Horizon Detection

本篇提出的损失函数反其道而行，总结出一般规律，再往回推出个例。

首先将旋转矩形转变成二维的高斯分布：

$$
m=(x,y)\\ Σ^{1/2}=RSR^T=\\ \begin{pmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{pmatrix} \begin{pmatrix} w/2 & 0 \\ 0 & h/2 \end{pmatrix} \begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix} \\= \begin{pmatrix} \frac{w}{2}cos^2⁡θ+\frac{h}{2}sin^2⁡θ & \frac{w-h}{2}cos\theta sin\theta \\ \frac{w-h}{2}cos\theta sin\theta & \frac{w}{2}sin^2⁡θ+\frac{h}{2}cos^2⁡θ \end{pmatrix}
$$

Gaussian Wasserstein Distance

$$
d^2=‖m_1−m_2 ‖_2^2+Tr(Σ_1+Σ_2−2(Σ_1^{1/2} Σ_2 Σ_1^{1/2})^{1/2})
$$

可以将GWD看成两个部分：第一个部分是中心点的偏差，第二个部分是其他参数的耦合项，所以该损失函数其实是一个半耦合的损失函数，并且它没有尺度不变性的特征；如果角度为0即90度，那么：

$$
D_w^h(N_p,N_t )^2=l_2−norm(Δx,Δy,Δw/2,Δh/2)
$$

Proposed Approach

Kullback-Leibler Divergence

两个高斯距离间的KL散度为:

$$
D_{kl} (N_p ||N_t )=\frac{1}{2}(μ_p−μ_t )^T Σ^{−1}_t(μ_p−μ_t )+\frac{1}{2}Tr(Σ_t^{−1}Σ_p)+\frac{1}{2}ln⁡(|Σ_t|/|Σ_p|)−1\\ D_{kl} (N_t ||N_p )=\frac{1}{2}(μ_t−μ_p )^T Σ^{−1}_p(μ_t−μ_p )+\frac{1}{2}Tr(Σ_p^{−1}Σ_t)+\frac{1}{2}ln⁡(|Σ_p|/|Σ_t|)−1
$$

虽然KL散度和GWD一样都是参数半耦合的，但是它有更好的中心点参数优化的机制，就拿第一种散度举例：

$$
(μ_p−μ_t )^T Σ^{−1} (μ_p−μ_t )=\frac{(4Δxcosθ_t+Δysinθ_t )^2}{w_t^2} +\frac{(4Δycosθ_t−Δxsinθ_t)^2}{h_t^2}\\ Tr(Σ_t^{−1}Σ_p)=\frac{h_p^2}{w_t^2}sin^2⁡Δθ+\frac{w_p^2}{h_t^2}sin^2⁡Δθ+\frac{h_p^2}{h_t^2} sin^2⁡Δθ+\frac{w_p^2}{w_t^2} cos^2⁡Δθ\\ ln⁡\frac{|Σ_t |}{|Σ_p|} =ln⁡\frac{h_t^2}{h_p^2}+ln⁡\frac{w_t^2}{w_p^2}
$$

Advanced Analysis

Analysis of high-precision detection

不失一般性，先列举角度为0即水平边框的情况：

$$
\frac{∂f_{kl}(μ_p )}{∂μ_p}=(\frac{4}{w_t^2}Δx,\frac4{h_t^2}Δy)^T
$$

通过上述式子可以发现，中心点的偏移是受到真实标签长宽的尺度影响。当不是水平情况的时候，除了水平边框之外还会根据角度进行动态的调整

而GWD和距离损失函数的形式为：

$$
\frac{∂f_w (μ_p )}{∂μ_p}=(2Δx,2Δy)^T\\ \frac{∂f_{L_2}(μ_p)}{∂μ_p}=(\frac{2}{w_a^2}Δx,\frac{2}{h_a^2}Δy)^T
$$

前者不能动态的根据真实标签的长宽去调整损失，后者是根据anchor的长宽去调整，也是不合理的。

除此之外：

$$
\frac{∂f_{kl}(Σ_p)}{∂ln⁡h_p}=\frac{h_p^2}{h_t^2}cos^2⁡Δθ+\frac{h_p^2}{w_t^2}sin^2⁡Δθ−1\\ \frac{∂f_{kl}(Σ_p)}{∂ln⁡w_p}=\frac{w_p^2}{w_t^2}cos^2⁡Δθ+\frac{w_p^2}{h_t^2}sin^2⁡Δθ−1
$$

如果角度为0，那么上面两个等式可以为:

$$
\frac{∂f_{kl}(Σ_p)}{∂ln⁡h_p}=\frac{h_p^2}{h_t^2}−1\\ \frac{∂f_{kl}(Σ_p)}{∂ln⁡w_p}=\frac{w_p^2}{w_t^2}−1
$$

这意味着真实标签长宽越小的时候，会有更大的loss出现，这是非常有必要的，越小的长宽需要越大的精度

另一方面：

$$
\frac{∂f_{kl}(Σ_p)}{∂θ_p}=(\frac{h_p^2−w_p^2}{w_t^2}+\frac{w_p^2−h_p^2}{h_t^2})sin2Δθ
$$

当预测值和真实值相等的时候：

$$
\frac{∂f_{kl}(Σ_p)}{∂θ_p}=(\frac{h_p^2}{w_t^2}+\frac{w_p^2}{h_t^2}-2)sin2Δθ≥sin2Δθ
$$

只有在真实标签为正方形的时候取等号，上面的式子也说明当长宽比很大的时候模型能对loss惩罚项更大。上面的等式可以看出当模型某一项参数进行优化的时候，其他参数会作为权重进行动态的调整，并且D_{kl} (N_p ||N_t ),D_{kl} (N_t ||N_p )两者的性质是相当的。

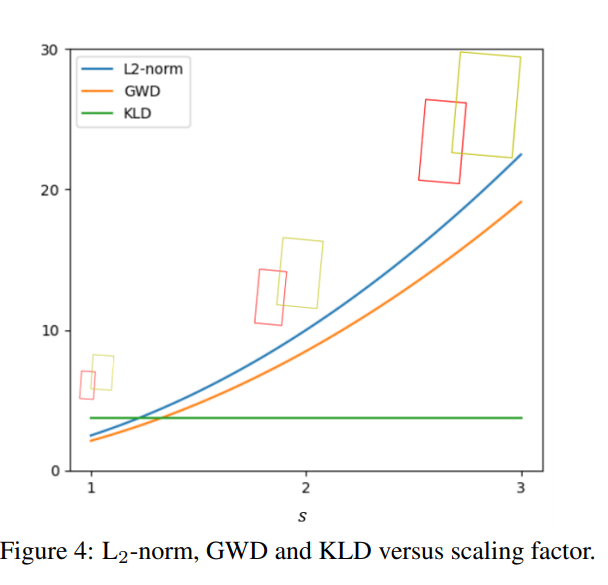
Scale invariance

该等式同时还具有尺度的不变性:

$$
D_{kl} (N_p ||N_t )=D_{kl} (N_{p’} ||N_{t'})\\ X_{p′}=MX_p\sim N_p (Mμ_p,MΣ_p M^T ),X_{p′}=MX_t\sim N_t (Mμ_t,MΣ_t M^T)\\
$$

当$M=kI$的时候就可以证明上述等式相等。

Variants of KLD

接下来介绍KLD散度的变体：

$$
D_{kl\_min⁡(max)} (N_p ||N_t )=min⁡(max)(D_{kl}(N_p ||N_t),D_{kl}(N_t ||N_p))\\ D_{js} (N_p ||N_t )=\frac{1}{2}(D_{kl}(N_t ||\frac{N_p+N_t}{2})+D_{kl} (N_p||\frac{N_p+N_t}{2}) )\\ D_{jef} (N_p ||N_t )=D_{kl}(N_t ||N_p )+D_{kl}(N_p ||N_t)
$$