ReDet

ReDet: A Rotation-equivariant Detector for Aerial Object Detection

Introduction

contribution

• 提出了Rotation-equivariant检测器用于高质量的遥感图像目标检测
• 设计了一个RiRoI Align从旋转同变性特征中提取旋转不变性特征

论文里提到的方法如下图所示：

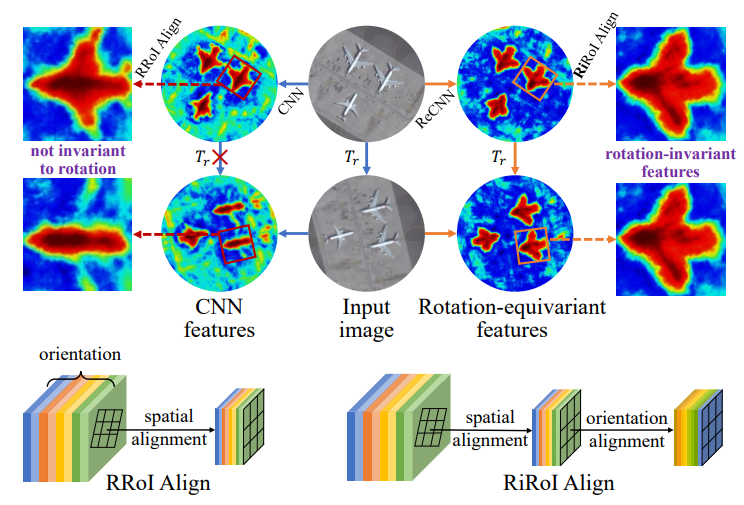
一共包含了两个部分：旋转同变性特征的提取和旋转不变性特征的提取

Preliminaries

同变性的等式可以列为：

$$
Φ[T_g^X (x)]=T_g^Y [Φ(x)]
$$

其中\(T_g\)表示在空间内相关操作，当所有的\(T_g^x\)和\(T_g^y\)都相同的时候同变性就成为了不变性。

而在卷积中的平移同变性可以用公式：

$$
[[T_t f]∗ψ](x)=[T_g [f∗ψ]](x)
$$

其中\(\psi:Z^2\rightarrow R^K\)代表的是卷积核并且\(*\)代表的是卷积操作，\(f\)代表的是特征图，\(T_t\)代表的是在空间上的相关操作

Rotation-equivariant Networks

旋转同变性网络和常规的CNN类似都是权重共享的，不论是平移的权重还是旋转的权重；假设在群G内\(\Phi=\{L_i|i\in\{1,2,...,M\}\}\)为一个有着M层旋转同变性的网络层，那么层\(L_i\in\Phi\)可以使旋转变化T_r得到保留\(L_i[T_r(g)]=T_r[L_i(g)],g\in G\)

整体的网络层可以表示为：

$$
[∏_{i=1}^ML_i ](T_r I)=T_r [∏_{i=1}^ML_i ](I)
$$

Rotation-invariant Networks

如果对于任何旋转变化，输入和输出的性质都保持相同，那么就可以认为输出特征具有旋转不变性，该特征主要可以分为图片级，实例级和像素级。

Rotation-equivariant Detector

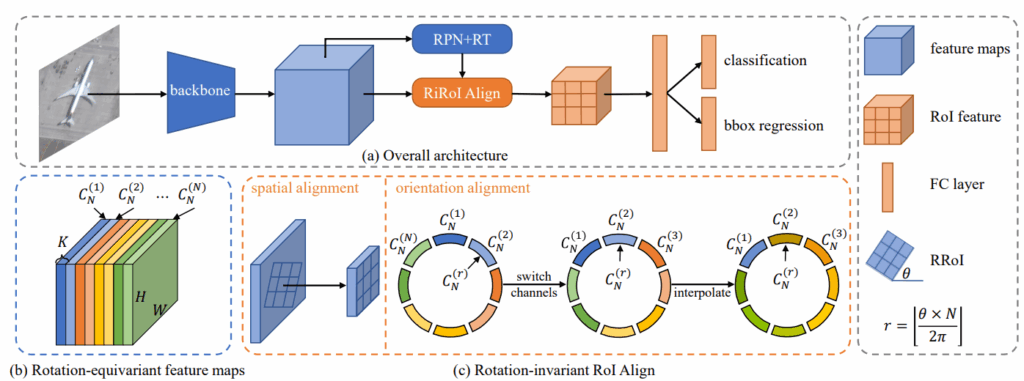
提出的架构整体如上图所示

Rotation-equivariant Backbone

仿照ResNet和FPN设计了ReResNet和ReFPN，基于e2cnn使用了旋转同变性的网络，不像传统网络该网络输出的特征图尺度为（K,N,H,W）有N个方向通道：

$$
f=\{f^{(i)}│i∈{1,2,…,N} \}
$$

每一个方向通道内，对应一个C_N元素。

该backbone的优点较为明显：

• 高度的权重共享
• 丰富方向信息
• 同计算量的情况下参数量更小

(ps:该backbone的主要两点就在于使用了e2cnn，但是e2cnn想要完全理解的话，必须得具有十分丰富的群论知识)

Rotation-invariant RoI Align

本次提出的RoI align方法除了继承RoI transformer的空间对齐同时还需要方向也对齐

具体来说对于输出的候选区域，方向对齐如下式表示：

$$
\hat{f}_R=Int(SC(f_R,r), θ),r=⌊θN/2π⌋
$$

其中SC和Int分别为交换通道和插值，对于候选区域的特征首先需要计算索引\(r\)将该索引对应的方向特征量提到最前面，但是一开始所设定的群都是离散的，如果角度并不在群内，那么需要离他最近的\(l\)个方向通道内的特征图进行插值。如果\(l\)为2话，插值公式为：

$$
\hat{f}_R^{(i)}=(1−α) f_R^{(i)}+αf_R^{(i+1)}\quad i∈[1,N]
$$

其中\(\alpha=\frac{\theta N}{2\pi}-r\)代表的是距离