ORConv

Oriented Response Networks

Introduction

本篇论文的贡献有以下几点：

• 提出了Activate Rotating Filter和orented Response Convolution
• 将上述结构融入到了常见的backbone之中

Oriented Response Networks

在卷积过程中旋转卷积核的方式来提取图片不同方向的特征，并且使用ARF后ORN需要的啊网络参数明显减少，并且支持明确的分层方向信息的编码

Active Rotating Filters

需要学习的只有标准的卷积核，其余卷积核的参数根据标准卷积核的参数进行相应的处理旋转的角度为\(\theta=2\pi n/N\)，其中\(n\in[1,N-1]\)，要得到旋转的卷积核一共分为两个步骤：

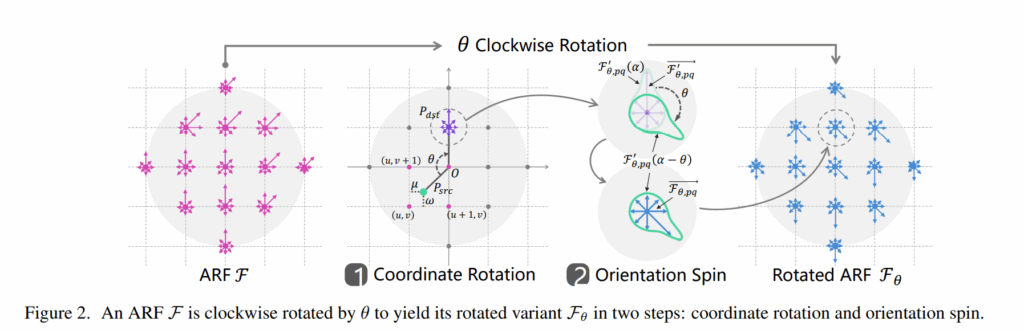
必要的参数为标准卷积核为，经过旋转之后卷积核表示为\(F_\theta\)

• 首先进行坐标系的旋转，旋转后的卷积核上坐标（p, q）可以旋转回标准卷积核上之后找到相应的坐标再经过双线性插值法找到具体的值；$$
  (p^′ q^′)=(p q) \begin{pmatrix} cos⁡(θ) & sin⁡(θ) -sin⁡(θ) & cos⁡(θ) \end{pmatrix}\\ \overrightarrow{F'_{θ,pq}}=(1−μ)(1−w) \overrightarrow{F_{μv}}+(1−μ)w\overrightarrow{F_{μ,v+1}}+μ(1−w) \overrightarrow{F_{μ+1,v} }+μw\overrightarrow{F_{μ+1,v+1}}
  $$

其中

$$
μ=⌊p'⌋,v=⌊q'⌋,u=p^′−u,w=q^′−v
$$

• 除了坐标之外还需要将方向也要进行相应的旋转，采用了傅里叶循环移位算法来进行相应的处理，这里作者一直在拿单通道的特征图举例：输出的八通道特征图可以看成一个点\(\overrightarrow{F'_{θ,pq}}\)上的八个方向的值，虽然空间域上已经进行了旋转，但是频率域上也要进行相应的移位操作$$
  X(k)≡DFT\{\overrightarrow{F'_{θ,pq}}^{(n)} \}=∑_{n=0}^{N−1}{F'_{θ,pq}}^{(n)}e^{−jk2πn/N},k=0,1,2…,N−1\\ \overrightarrow{F_{θ,pq}}^{(n)}≡IDFT\{X(k) e^{−jkθ} \}=1/N ∑_{k=0}^{N−1}X(k) e^{jk(2πn/N−θ)},n=0,1,…,N−1
  $$
  拿一个\(3*3*8\)的ARF举例一个标准卷积核的旋转版本可以表示为：$$
  \overrightarrow{\hat F'_{θ,<i>}} =\overrightarrow{\hat F'_{θ,<(i−k)mod N>} },i∈I\\ \overrightarrow{\hat F'_{θ}}=\overrightarrow{\hat F'^{(n−k) mod n}},n=0,1,…N−1
  $$

其中

$$
θ=k 2π/N,N=8,I=\begin{pmatrix} 7 & 0 & 1 \\ 6 & & 2 \\ 5 & 4 & 3 \end{pmatrix}
$$

I 代表卷积核上的坐标

Oriented Response Convolution

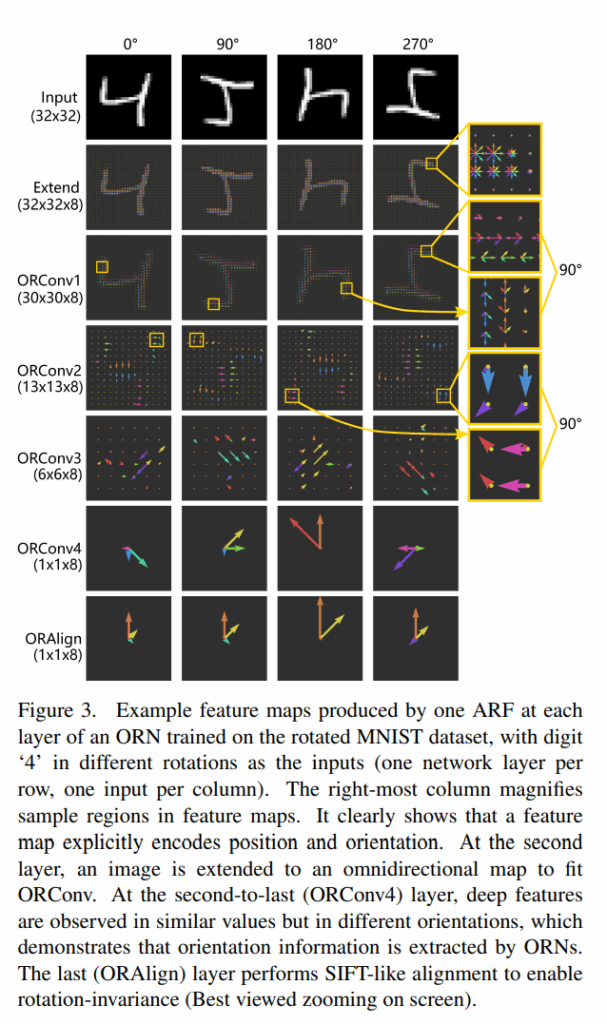
如果一个ARF的尺寸为\(W\times W\times N\)那么输入特征图通道为N（单通道举例）就应该可以看成一个点上的N个方向的值，ARF表示为F，输入特征图表示为M输出的特征图可以表示为

$$
\tilde M ̃=ORConv(F,M)\\ \tilde M^k=∑_{n=0}^{N−1}F_{(θ_k)}^{(n)}∗M^{(n)} \\θ_k=k2π/N,k=0,1,2,…,N−1
$$

Updating Filters

更新梯度的方式为(所以其实还是需要学习的，只不过学习完毕之后再将其通过角度还原)：

$$
δ^k=∂L/(∂F_(θ_k ) ),θ_k=k2π/N,k=0,1,2,..,N−1\\ F⟵F−η∑_0^{−1}δ_{−θ_k}^{(k)}
$$

Rotation Invariant Feature Encoding

为了提取出旋转不变性的特征，这里使用了两种方式ORAlign ORPooling，ORAlign是找到每个方向对应的特征图最大值（这里默认特征图尺寸已经到了\(1*1\)），找到最大值的对应特征将其旋转相应的角度，或者利用ORPool直接提取出最大的那个特征。