DAL

Dynamic Anchor Learning for Arbitrary-Oriented Object Detection

Introduction

通常在anchor-based的模型中，定义正负anchor的标准通常是IoU越大，则是正样本否则就是负样本。这个方法有一些问题，如下图所示：

具有很高IoU的anchor最终回归出来的效果并不很尽如人意，相反有些较低IoU的anchor却能回归出不错的效果，所以其实回归能力和anchor并不能完全画等号。并且从下图作者还可以得出以下的观点：

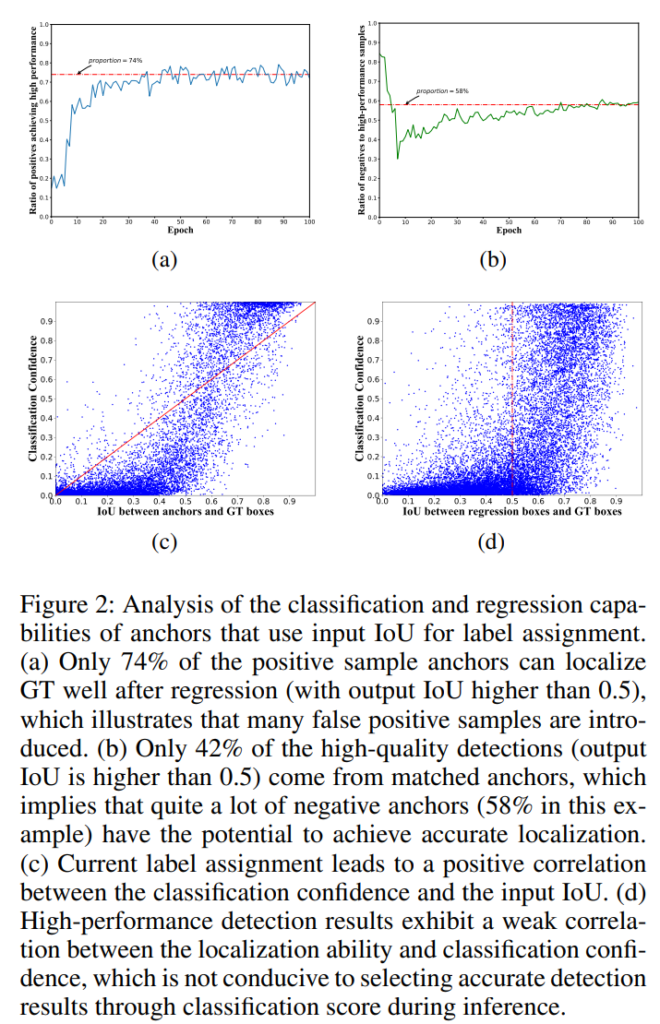
• 只有74%的正样本有很好的定位能力，这意味着其实有很多负样本也加入了进来
• 只有42%的正样本anchor回归后IoU占比超过0.5，其他全都来自负样本
• 现在的类别分配方式会使得置信度和IoU的值呈正相关
• 高性能的检测结果呈现出一种置信度和回归能力的弱相关性

本篇文章的贡献主要有以下几点：

• 观察到基于 IoU 在锚点和 GT 框之间的标签分配导致定位能力评估不理想，并进一步带来不一致的分类和回归性能
• 引入匹配度来衡量anchors的定位潜力
• 提出了matching-sensitive loss来缓解分类和回归之间相关性弱的问题，提高对高质量proposal的区分能力

Proposed Method

Rotation Detector Built on RetinaNet

编码方式为常规的编码方式，角度做差之后再取tan，（这里提到的loss让我产生了一丝丝的怀疑，先暂时按下不表）

Dynamic Anchor Selection

之前的相关文章已经有提及对于不同方向和长宽比的GT，不同部分的回归能力是不一样的，并且也有相关文章提到需要利用output IoU来动态的指导训练过程，但是如果直接使用output IoU会发现很难收敛，总结原因有以下几点：

• 输入IoU高但输出IoU低的anchors不一定都是负样本，可能是训练不充分造成的
• 意外获得准确定位性能的低质量锚点往往会被误判为正样本

不能有效利用高质量的样本，选择的假阳性样本会导致训练不稳定。

基于上述的观察，所以作者引入了匹配度的概念：

$$
md=α⋅sa+(1−α)⋅fa−u^γ,u=|sa−fa|
$$

其中sa为输入的IoU,fa为预测之后的IoU, u为不确定度，其中 \(\alpha\)参数为：

$$
\alpha(t) = \begin{cases} 1, & t<0.1 \\ 5(\alpha_0-1)\cdot t+1.5-0.5\alpha_0, & 0.1\le t \le 0.3\\ \alpha_0,&t\ge0.3 \end{cases},\\t=iters/Max
$$

Matching-Sensitive Loss

$$
L_{cls}=1/N ∑_{i∈ψ}FL(p_i,p_i^∗)+1/N_p ∑_{j∈ψ_p}w_j⋅FL(p_j,p_j^∗)
$$

其中,\(\psi\),\(\psi_p\)分别为所有anchor，以及正样本anchor，\(w_j\)为匹配的补偿因子补偿因子的计算方法为：对于每个gt，计算所有anchor的匹配度\(md\)以及正样本的匹配度\(md_{pos}\)，所有\(md\)匹配度最高的为\(md_{max}\)，则 \(\Delta md=1-md_{max}\)，最终的回归损失函数为：

$$
L_{reg}=1/N_p ∑_{j∈ψ_p}w_j⋅L_{smoothL1}(t_j,t_j^∗)
$$