Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
1 Introduction
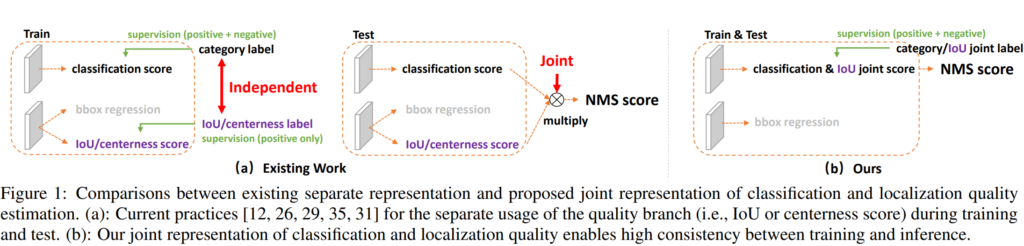
作者写本文的动机：
- 定位和分类的不连续：首先定位和分类、centerness（IoU）都是分别训练的，但是推理的时候却开始互动了；有可能出现分类的质量很低，但是centerness或者IoU很高的情况
- 现有模型的回归方式并不灵活，是一种很hard的回归方式
因此作者提出了GFL，这种GFL loss方式可以被特化为QFL与DFL用于分类和定位
GFL的好处：
- 打破了训练和推理的不一致性
- 可以更好的定位bbox的位置
Method
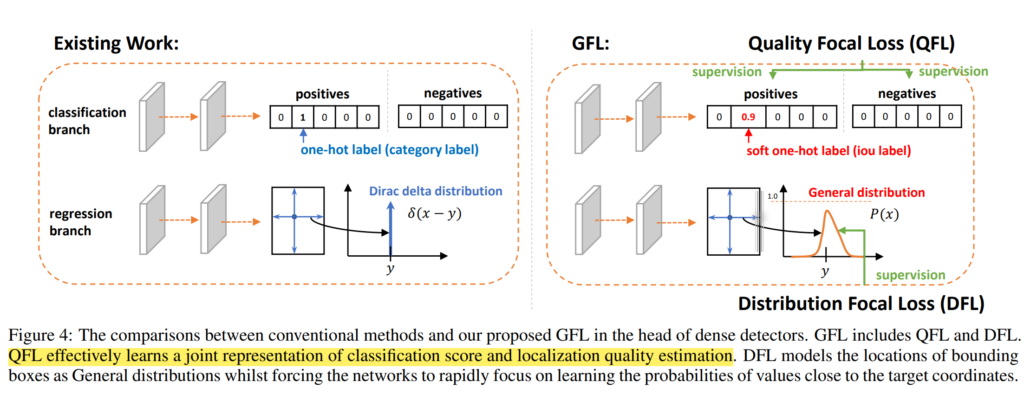
Quality Focal Loss (QFL)
作者根据FL得到了新的QFL，普通的分类是非常hard的一种方式，并且没有结合IoU或centerness，所以作者选择将这两种方式结合在一起，即对应的位置gt不再是单纯的0或者1，而是IoU，而这里的IoU是关于预测的bbox和对应的gt生成的IoU，最终loss可以表示为
$$
QFL(σ)=−|y−σ|^β ((1−y)log(1−σ)+ylog(σ))
$$
Distribution Focal Loss (DFL)
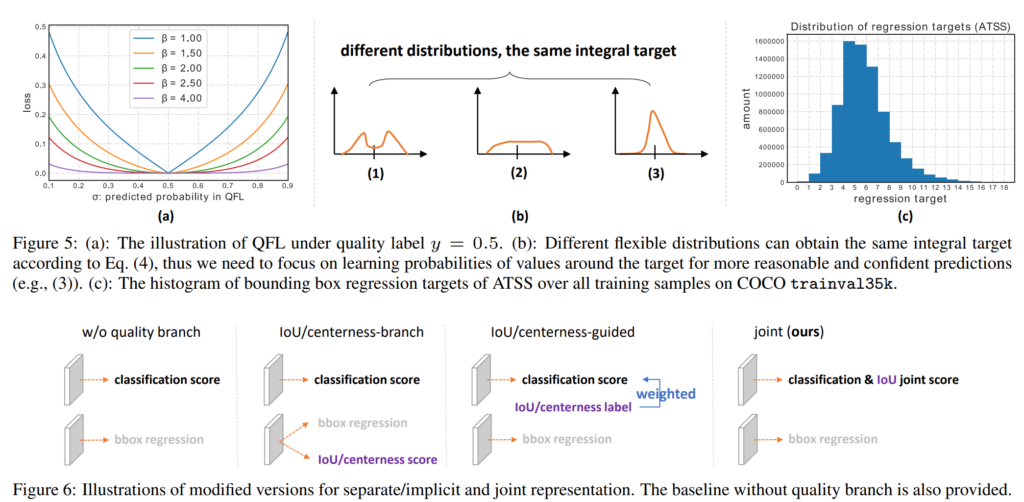
关于bbox的回归，作者选择了直接预测分布的方式，由于概率分布的积分和是一但是积分上下限是正负无穷，所以先规定了积分的上下限之后再进行离散化处理。
$$
y ̂=∫_{−∞}^∞P(x)xdx=∫_{y_0}^{y_n}P(x)xdx
$$
$$
y ̂=∑_{i=0}^nP(y_i)y_i
$$
但是如果直接这么预测分布（其实还是通过softmax进行处理）对模型的收敛性会造成很大影响，所以
$$
GFL(p_{y_l},p_{y_r})=−|y−(y_l p_{y_l}+y_r p_{y_r} )|^β ((y_r−y) log(p_{y_l})+(y−y_l )log(p_{y_r}))
$$
最终损失函数为
$$
L=1/N_{pos} ∑zL_Q +1/N{pos} ∑_{1_{c_z^∗>0}} (λ_0 L_B+λ_1 L_D)
$$