FAR

Frequency Autoregressive Image Generation with Continuous Tokens

概览

以MAR为基础（需要注意的是，作者提到VAR的token是离散的，本文使用的是连续的，原因：信息损失以及压缩率），但是将尺度替换成了频率

整体框架如下图所示：

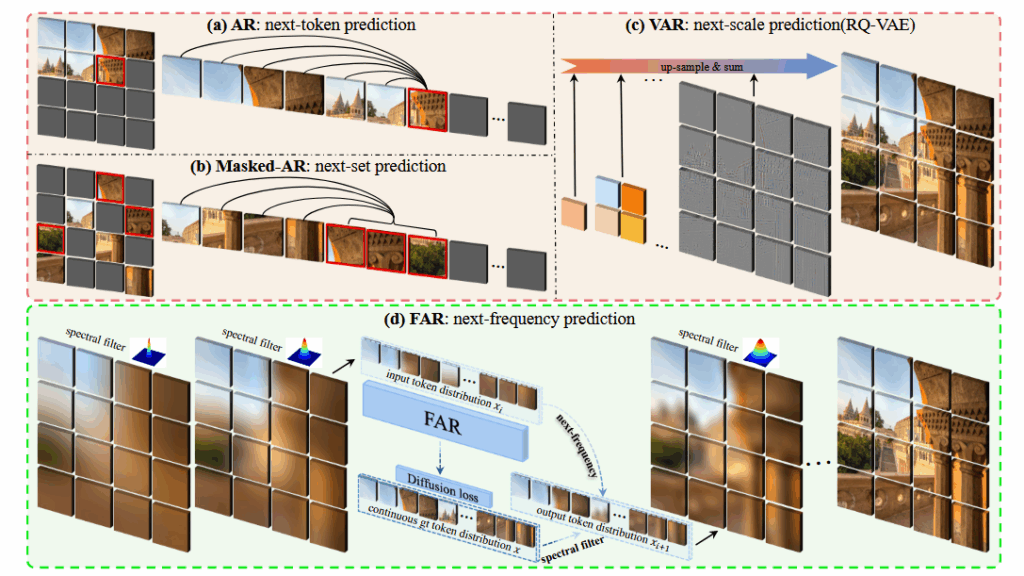
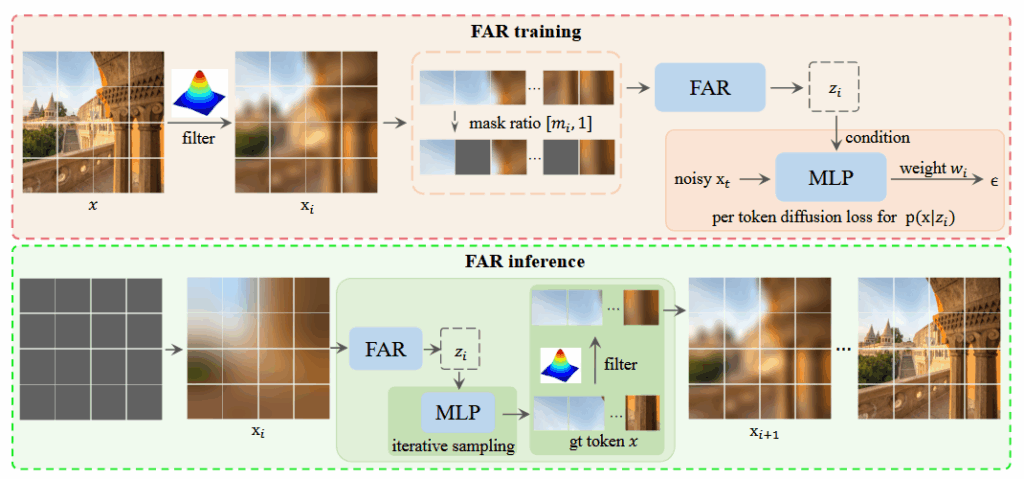
方法

频谱依赖：在自回归图像生成的回归方向问题中，核心挑战在于如何协调因果序列要求与图像的固有先验。本文将频谱依赖视为一种适用于此场景的独特图像先验。

具体而言，图像由低频成分和高频成分组成：

低频成分：捕捉整体亮度、颜色和形状等基础结构。

高频成分：传达边缘、细节和纹理等精细信息。 高频信息的生成本质上依赖于低频信息的先验建立。

（神经网络自然会优先学习低频信息，再逐步处理更复杂的高频细节）

下一频率预测的自回归图像生成利用频谱依赖性，为自回归图像生成引入了创新的下一频率预测方法。对于每幅图像$x$，其在频率级别$i\in{1,2,\ldots,F}$的中间输入形成如下：

$$ x_{i}=\mathcal{F}^{-1}M_{i}\mathcal{F}x $$

其中：\(F\)表示频率级别数，\(\mathcal{F}\)和\(\mathcal{F}^{-1}\)分别表示傅里叶变换和逆傅里叶变换, \(M_{i}\)表示第\(i\)级的频谱滤波器。频率级别\(i\)​越高，保留的高频信息越多

不同频率级别下标记分布建模的优化难度和方差，引入掩码机制以提高训练效率，并提出了频率感知扩散采样策略以加速推理

简化扩散损失的分布建模: 连续标记器中的扩散损失对每个标记的分布进行建模。对于FAR，扩散损失需要为\(i\in[1,F-1]\)建模\(p(x_{i+1}|x_{i})\)，涵盖\(F\)个频率级别。这种多层级的分布建模对于相对较小的MLP网络来说具有挑战性。直接为\(i\in[1,F-1]\)建模\(p(x|x_{i})\)，然后对\(x\)进行滤波以得到\(x_{i+1}\)。这种方法通过将扩散损失放宽到仅对\(x\)进行建模，简化了优化复杂度。

优化方差：频率感知训练损失策略, 不同的频率级别呈现出不同的优化难度。具体而言，高频输入更容易预测，这可能导致优化过程被更具挑战性的低频级别所主导，从而阻碍高频细节的学习。使用频率感知训练损失策略，为高频级别分配更高的损失权重，以确保所有频率的学习平衡。

具体而言，损失权重按正弦曲线实现如下：

$$w_{i}=1+\sin\left(\frac{\pi}{2}×\frac{i}{F}\right)$$

其中，\(w_{i}\)是频率级别\(i\)的损失权重。

训练效率：设计一种频率感知掩码策略，对较低频率级别逐步增加掩码比例。掩码机制为频率级别\(i\)的输入标记随机掩码\([r_{i},1]\)个输入标记，其中\(r_{i}\)从0.7线性变换到0。

作者提到有两种方法可以筛选频率，一种是空间中下采样再上采样，另一种使用傅里叶频域操作，两种方法最终的效果都差不多，所以就选择了第一种